-
- Sale!
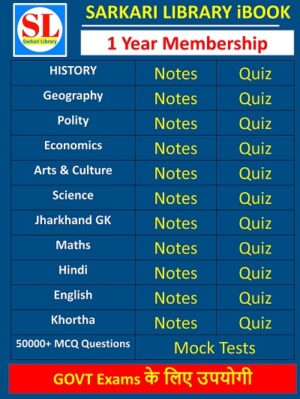
- Membership
1 Year Membership
- Original price was: ₹300.00.₹210.00Current price is: ₹210.00.
- Buy Now
-
- Sale!
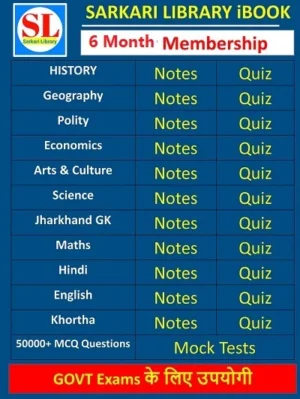
- Membership
6 Month Membership
- Original price was: ₹200.00.₹120.00Current price is: ₹120.00.
- Buy Now
Shop
This is where you can browse products in this store.